如何お過ごしですか? 3回連続10cmです。
当ブログにお越しいただきありがとうございます。
いつも本当にありがとうございます。
地味な土木小ネタシリーズ。
妙なタイトルなんですが、今回は『道路の縦断曲線』の話です。
人生山あり谷あり、道路も山あり谷あり。
みなさまも経験されているように人生は平たんではありません。
上り調子の時もあれば下り調子の時もあります。
これは世の常です。
道路だって同じなんです。
上り坂もあれば下り坂もあります。
峠があれば上り坂になるし、峠を越えて平野に戻る時には下り坂、また峠があれば上り坂。
上っては下り、下っては上る。
これのくり返しです。
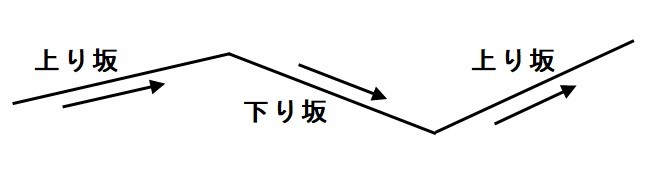
この上り・下りを縦断と言います。
(これテストに出まーす!)
その上り坂と下り坂の境目がポキっと折れていたら。
上り坂と下り坂の境目がもしポキっと折れていたら(これは極端な例ですが)こななりますやん。
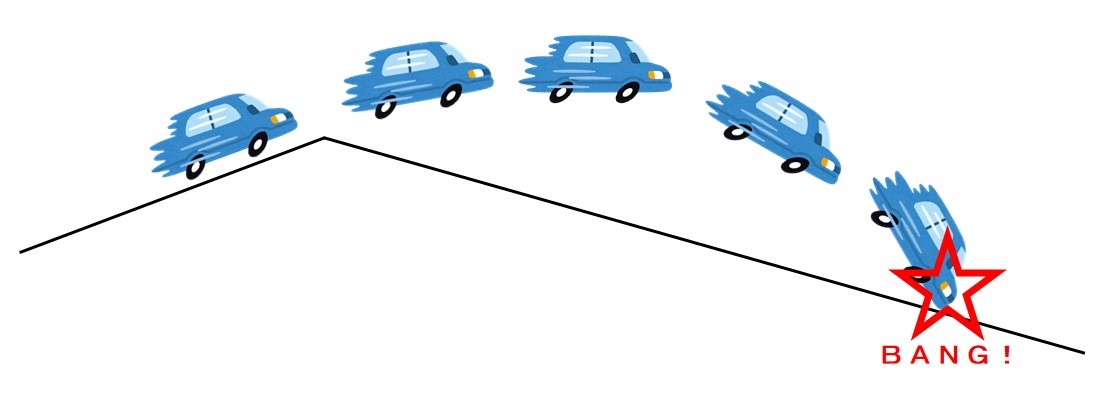
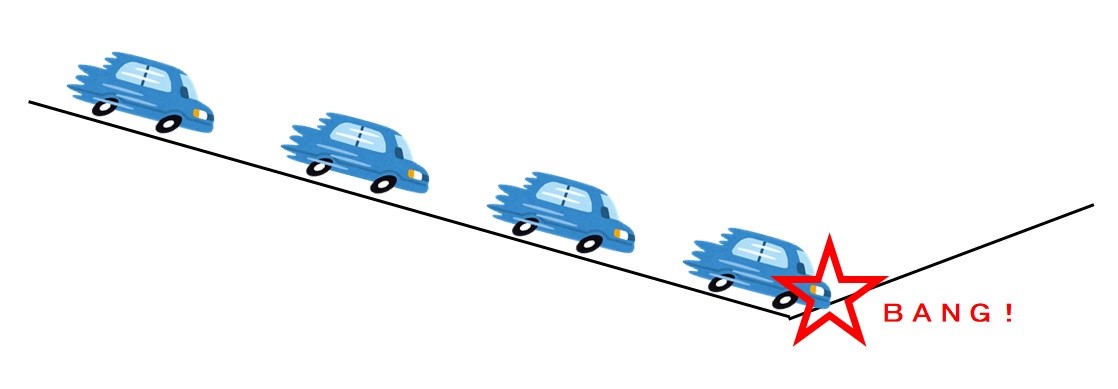
これはいただけませんよね。
じゃどななってんの?
ポキっと折れている所を滑らかにつなぐ曲線が入っています。
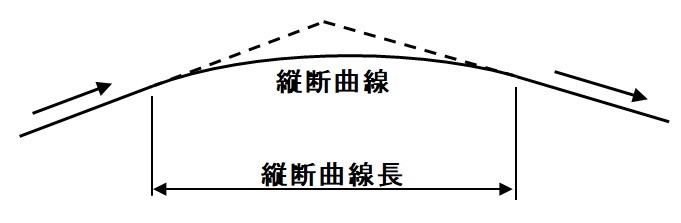
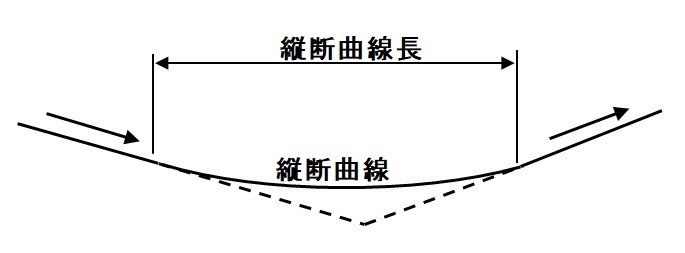
その曲線のことを縦断曲線と言います。縦断曲線は2次放物線です。
またその曲線の長さ(=曲線の範囲)を縦断曲線長と言います。
(これもテストに出まーす!)
ちなみに道路には道路規格(=道路の格付けみたいなの)というものがあって、(簡単に言うと)市町村道→都道府県道→国道→高速道路というように概ね自動車の速度によって規格が上がっていきます。
例えば制限速度が40km/hの市町村道よりも100km/hの高速道路の方が規格が高いということです。
縦断曲線や縦断曲線長は道路規格によって大小が決められています。
縦断曲線や縦断曲線長は道路規格が低いほど値が小さく、道路面はそんなに滑らかではなく、
道路規格が高くなるほど値が大きく、道路面がより滑らかになります。
制限速度に応じた滑らかさにしています。
これだと(制限速度を守ればの話ですが)自動車もBANG!しませんね。
参考資料(ムズいです)。
縦断曲線中の任意の点(C点)の高さを求める。
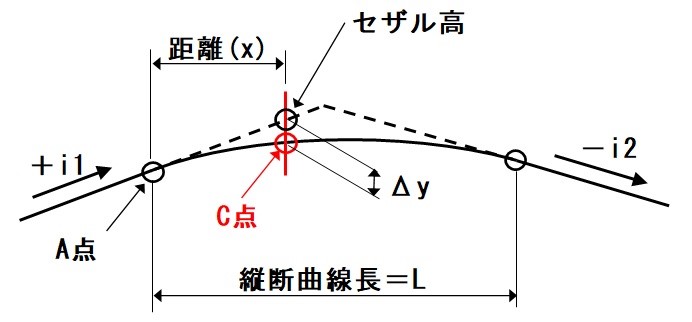
セザル高=A点の高さ+i1×距離(x)
Δy={|(+i1)-(-i2)|/200・L}×距離(x)^2
任意の点C点の高さ=セザル高-Δy
例題:
i1=5.0%、i2=-5.0%、
A点の高さ=20.0、距離(x)=10.0、
縦断曲線長L=50.0
の場合の任意の点C点の高さは
セザル高=20.0+5.0/100×10.0=20.5
Δy={|(5.0)-(-5.0)|/200×50.0}×10.0^2=0.1
任意の点C点の高さ=20.5-0.1=20.4
編集後記
道路の縦断や縦断曲線はいかがでしたか?
楽しんでいただけましたか?
実際に道路を走っていてもあまり気にされないと思いますが、我々は気にしています(笑)
それではみなさま、よい縦断曲線ライフをお送りください。
ブログ村のランキング参加中。
クリックありがとうございます。えへへ
↓ ↓ ↓![]() にほんブログ村
にほんブログ村

